HEXÁGONO DADO EL LADO
HEXÁGONO DADO EL LADO
 PASOS:
PASOS:
- Dibujamos el segmento AB, que es uno de los lados del hexágono, en nuestro caso de 3 cm.
- Hacemos centro de compás en A y en B con radio 3 cm. y donde se nos corten esos dos arcos obtenemos el punto O.
- O será el centro de la circunferencia que circunscribirá al hexágono de lado el segmento AB.
- Hacemos centro de compás en el punto O con radio hasta A y dibujamos la circunferencia.
- Con radio 3 cm., marcamos en la circunferencia los demás vértices del hexágono.
- Una vez obtenidos los vértices del hexágono, sólo nos queda unirlos.
HEPTÁGONO DADO EL LADO

PASOS:
- Dibujamos el segmento AB, que es uno de los lados del heptágono, en nuestro caso de 2,5 cm.
- Hacemos una perpendicular al segmento AB que pase por B.
- Hacemos la mediatriz del segmento AB.
- Hacemos centro de compás en A con abertura hasta B y donde nos corte a la mediatriz obtenemos el punto 2.
- Unimos A con 2, dibujando un ángulo.
- Hacemos la bisectriz de ese ángulo.
- Donde la bisectriz nos corte a la perpendicular a AB trazada por B, obtenemos el punto 3.
- Hacemos centro de compás en A con abertura hasta 3, y donde ese arco nos corte a la mediatriz obtenemos el punto O.
- O será el centro de la circunferencia que circunscribirá al heptágono de lado el segmento AB.
- Hacemos centro de compás en el punto O con radio hasta A y dibujamos la circunferencia.
- Con radio 2,5 cm., marcamos en la circunferencia los demás vértices del heptágono.
- Una vez obtenidos los vértices del heptágono, sólo nos queda unirlos.
OCTÓGONO DADO EL LADO
PASOS:
- Dibujamos el segmento AB, que es uno de los lados del octógono, en nuestro caso de 2,5 cm.
- Hacemos la mediatriz del segmento AB.
- Haciendo centro de compás en el punto medio del segmento AB y radio hasta A o B hacemos un arco de circunferencia.
- Donde ese arco de circunferencia nos corte a la mediatriz del segmento AB obtenemos el punto 1.
- Haciendo centro de compás en 1 con radio hasta A dibujamos una cirunferencia.
- Donde esa circunferencia nos corte a la mediatriz del segmento AB obtenemos el punto O.
- O será el centro de la circunferencia que circunscribirá al octógono de lado el segmento AB.
- Hacemos centro de compás en el punto O con radio hasta A y dibujamos la circunferencia.
- Con radio 2,5 cm., marcamos en la circunferencia los demás vértices del octógono.
- Una vez obtenidos los vértices del octógono, sólo nos queda unirlos.


MÉTODO GENERAL POLÍGONOS INSCRITOS
http://www.aulafacil.com/cursos/l5618/secundaria-eso/dibujo-lineal-secundaria/educacion-plastica-y-visual-2-eso/construccion-de-poligonos-regulares-inscritos-en-una-circunferencia-aplicando-el-teorema-de-thales-metodo-general
Este procedimiento se utilizará solo cuando el polígono buscado no tenga una construcción particular, ni pueda obtenerse como múltiplo de otro, dado que este procedimiento lleva inherente una gran imprecisión.
Sirve para dibujar polígonos inscritos en una circunferencia de cualquier número de lados.
A mayor sea el número de lados, mayor será la imprecisión.
En nuestro caso lo vamos a utilizar para dibujar un eneágono inscrito en una circunferencia de radio 3,5 cm.

PASOS
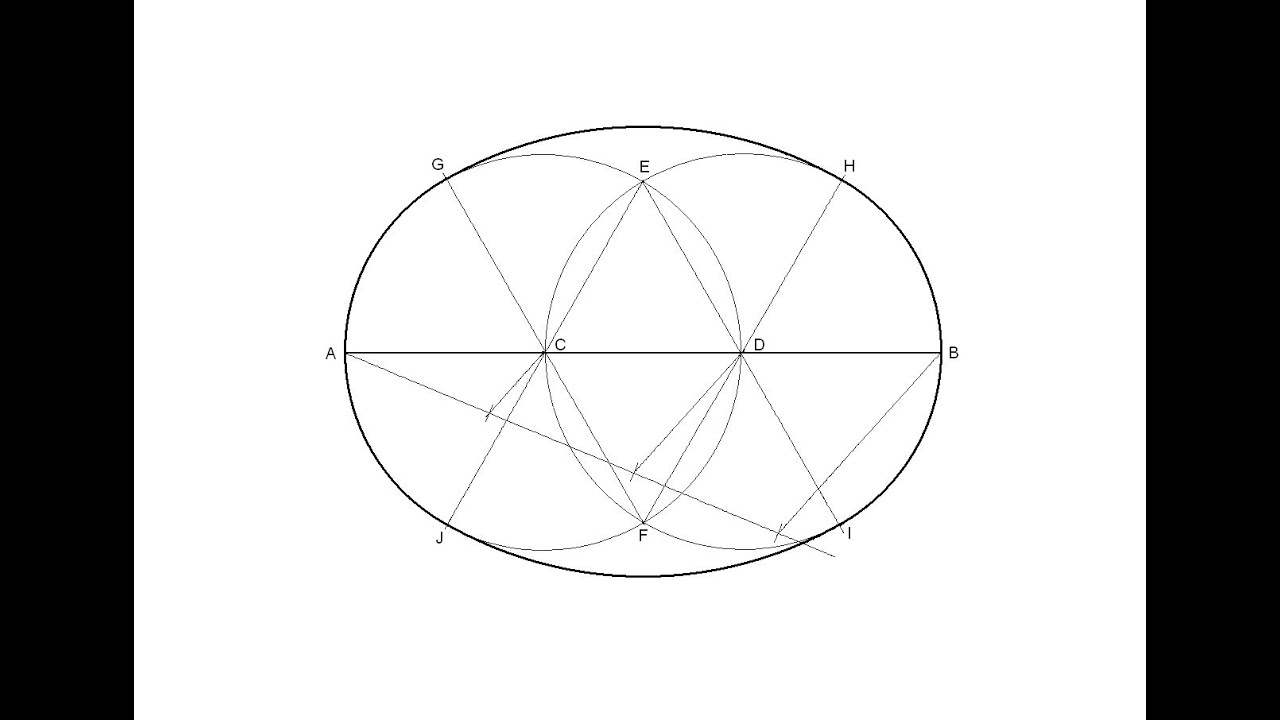
- Dibujamos la circunferencia en la que vamos a inscribir el eneágono, en nuestro caso de radio 3,5 cm.
- Dibujamos sus diámetros vertical usando la escuadra y el cartabón.
- Dividimos el diámetro en nueve partes iguales utilizando Tales.
- Hacemos centro de compás en los dos puntos de intersección del diámetro con la circunferencia con radio el diámetro y dónde se nos corten obtenemos el punto 1.
- Unimos el punto 1 con el punto de la segunda división del diámetro, y dónde esa semirrecta nos corte a la circunferencia obtenemos un vértice del eneágono, B.
- Ahora ya conocemos el lado del eneágono inscrito en una circunferencia de radio 3,5 cm.
- Con radio AB, vamos marcando el resto de los vértices del eneágono en la circunferencia.
- Una vez obtenidos los vértices del eneágono, sólo nos queda unirlos.
MÉTODO GENERAL DADO EL LADO
Para trazar un polígono regular de cualquier número de lados inscritos en una circunferencia dada, seguiremos los siguientes pasos :
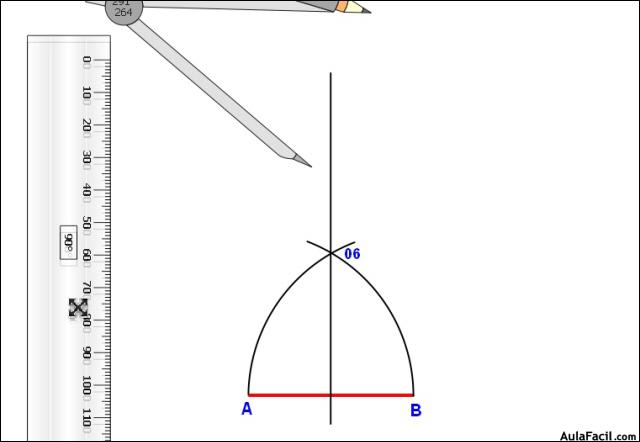
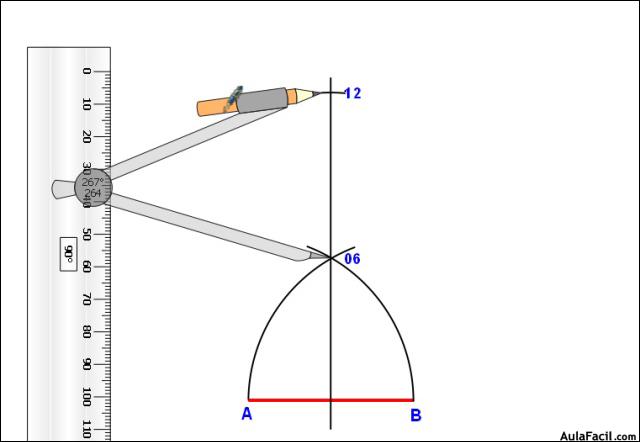
1. Hallar la mediatriz del lado AB y trazar un arco con centro en A o en B y con radio el lado, hasta cortar a la mediatriz en un punto que llamamos O6.
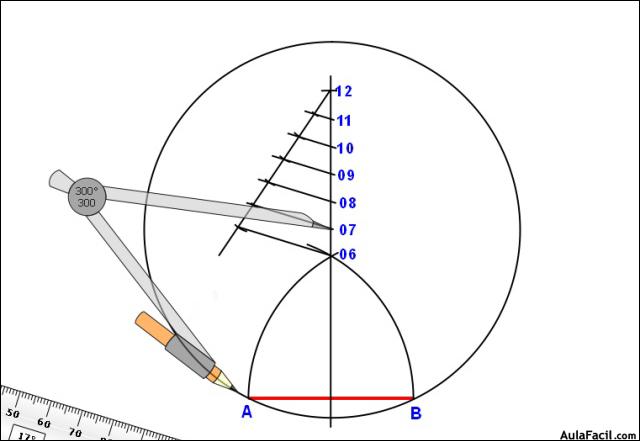
2. Con centro en O6 y radio el lado AB trazamos un arco auxiliar hasta cortar a la mediatriz en un punto que llamamos 12.
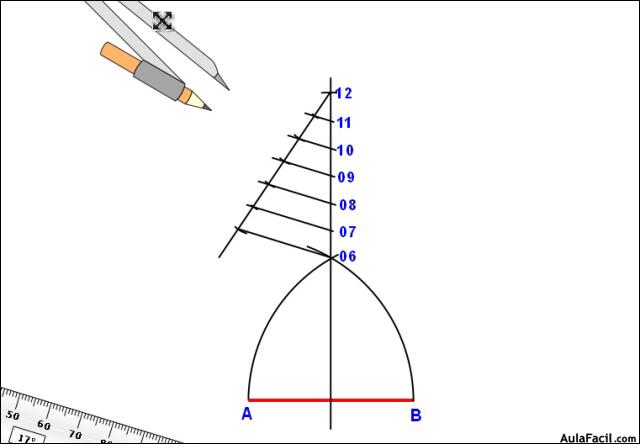
3. Se divide el segmento O6-12 en 6 partes iguales por medio del Teorema de Thales.
4.Cada una de las divisiones obtenidas entre 06 y 012, es decir 07,08,09...012, son centros de sus polígonos respectivos, así si queremos trazar el polígono de 6 lados sólo tenemos que centrar el compás en 06 y con radio 06-A, trazar la circunferencia que contendrá a ese polígono. Si tenemos que trazar el polígono de 8 lados, sólo habrá que centrar el compás en 08 y con radio 08-A trazar la circunferencia que contendrá al octógono... y así sucesivamente. En nuestro caso haremos el de 7 lados.